题解: SICP-learning/exercise_1 at master · booiris/SICP-learning · GitHub

1. Building Abstractions With Procedures

sicp 前面部分介绍的内容还是比较基础的，具体是在介绍程序是什么。

We are about to study the idea of a computational process. Computational processes are abstract beings that inhabit computers. As they evolve, processes manipulate other abstract things called data. The evolution of a process is directed by a pattern of rules called a program.

– computational process (即计算过程) 是操作数据的过程，这一过程的实现由一组定义的规则(程序)完成。

从中可以看出编写的计算机程序有两个重要的元素:

  1. 数据
  2. 操作数据的行为

笔者认为我们编写的程序就是处理数据的过程，是对数据的各种加工变换(这就是为啥一个好的类型系统那么重要，土法炼钢不可取，此处@某一个大道至简的语言😚为啥 go 不支持泛型方法)。

1.1 The elements of Programming

本节开始又到了最喜欢的概念定义环节，一个成熟的语言需要以下三种结构：

  1. primitive expressions, which represent the simplest entities the language is concerned with,
  2. means of combination, by which compound elements are built from simpler ones, and
  3. means of abstraction, by which compound elements can be named and manipulated as units.

具体来说就是需要

  1. 基本表达式，表示语言中的一些基础的实体，比如变量和基本类型等
  2. 组合算子，能够从简单的元素构建出复杂的运算，比如运算符和函数调用等
  3. 抽象方式，能够将一组过程或者数据类型封装合并为一个单元，比如变量定义、函数定义和抽象数据类型的定义

之后，文中再次强调了程序中最重要的两个元素，过程和数据(但实际上过程也可以认为是一种数据(有没有函数是一等公民的即视感) )：

In programming, we deal with two kinds of elements: procedures and data. (Later we will discover that they are really not so distinct.)

1.1.1 Expressions

基本上是在通过介绍 lisp 中的一些语法来阐释 expressions 这一概念（不过 lisp 是前缀表达式还真是反直觉👾，当然把运算符当成函数调用看能好一点，也确实能更好表达函数复合等概念，但还是难受🤖）。

一些表达式例子:

1
2
3
123
(+ 1 2)
(* (+ 1 2) 4)

后面带运算符的表达式被称为组合式。

1.1.2 Naming and the Environment

介绍了 lisp 的变量定义方式，还捎带讲了下变量作用域的概念。

1.1.3 Evaluating Combinations

介绍了 lisp 计算组合式的方式：

  1. 计算组合式需要首先计算所有子表达式，是一个递归计算的过程。
  2. 自左向右计算值。

计算组合式的过程构成了一个多叉树，计算组合式的过程就是计算一个个基本表达式的过程，而构成基本表达式的规则为：

  1. 数值的值就是它们所代表的数字本身 (有点怪怪的，应该指的是 数值是最基本的元素，参与运算的实际上是具体的数值。比如计算 x=2， + x 1 时，实际上是计算 + 2 1，在计算的过程中变量已经替换为具体的值了)。
  2. 表达式中有一些基本内置运算符，对应着完成相应操作的机器指令。
  3. 表达式中还存在着一些变量，这些变量指向当前作用域中的一个特定对象。所以变量不能脱离作用域，单纯的 (+ x 1) 是无意义的，无法计算出它的值。

1.1.4 Compound Procedures

这一章介绍的是 lisp 中函数的定义方法，在文中被称为 “compound procedure”。

lisp 的函数定义语法形式为：

1
( define (<name> <formal parameters>) <body> )

1.1.5 The Substitution Model for Procedure Application

本章讲的是 lisp 计算自定函数的过程，和 1.1.3 Evaluating Combinations 中计算组合式的过程类似。在本章中使用了 “substitution model” (替换)来解释运算过程。

例:

对于如下函数

1
2
3
4
5
(define (square x) (* x x) )
(define (sum-of-squares x y)
	(+ (square x) (square y) ) )
(define (f a)
	(sum-of-squares (+ a 1) (* a 2) ) )

计算 (f 5) 的过程如下:

1
2
3
4
5
6
7
(f 5) ->
(sum-of-squares (+ 5 1) (* 5 2) ) ->
(sum-of-squares 6 10) ->
(+ (square 6) (square 10) ) ->
(+ (* 6 6) (* 10 10) ) ->
(+ 36 100) ->
136

substitution model 就是将实际的运算式替换函数名的过程。但这并不是lisp 的实际运算过程。在后续 3、4、5 章会更详细地讲述这一过程。

计算表达式的顺序

在上面举例计算 (f 5) 的过程中可以发现，我们是在遇到可计算的基本表达式时就直接计算出对应的值。然而还有另一种计算的方式，就是在计算表达式的过程中只展开表达式，而不计算值，当整个表达式被展开成只由基本表达式组成时，再计算出值。

1
2
3
4
5
(f 5) ->
(sum-of-squares (+ 5 1) (* 5 2) ) ->
(+ (square (+ 5 1)) (square (* 5 2) ) ) ->
(+ (* (+ 5 1) (+ 5 1) ) (* (* 5 2) (* 5 2) ) ) ->
136

这种完全展开的计算过程被称为 normal-order evaluation (正则序求值)，先求值再代入函数调用的被称为 applicative-order evaluation (应用序求值)。

lisp 中采用的是后面一种计算方式，部分原因在于其能够避免对表达式的重复求值。对于人类来说，完全展开然后计算从直觉上感觉就十分麻烦，但其也有特殊用处，可以用于处理无法求值的表达式，第三章讨论了使用正则式定义的流式过程，用于处理无限数据结构。

1.1.6 Conditional Expressions and Predicates

这一章介绍了 lisp 中的分支语法，语法形式为：

1
2
3
4
(cond (⟨p₁⟩ ⟨e₁⟩)
      (⟨p₂⟩ ⟨e₂⟩)
      …
      (⟨pₙ⟩ ⟨eₙ⟩))

还有个 if 语法糖，语法形式为：

1
(if ⟨predicate⟩ ⟨consequent⟩ ⟨alternative⟩)

分支语法关联的逻辑运算符为：

1
2
3
(and ⟨e₁⟩ … ⟨eₙ⟩)
(or ⟨e₁⟩ … ⟨eₙ⟩)
(not ⟨e⟩)

1.1.7 Example: Square Roots by Newton’s Method

首先，如 1. Building Abstractions With Procedures 中所言，procedures 是操作数据的过程，这很像常规的数学函数，通过输出一些值，经过一些运算然后得到一些值。但和数学上的函数不一样的点在于，程序中的函数必须是可行的。

以计算平方根为例，在数学上定义平方根 yy 为

y=x,wherey≥0andy2=xy = \sqrt{x} , \quad where \quad y \geq 0 \quad and \quad y^2 = x

非常的清晰，但也非常的抽象，这个函数只给出了什么是平方根函数(平方的逆函数)，但并没有给出怎么计算一个值的平方根。在书中提到这反映了说明性描述和过程性描述的区别，即使给出了一个函数的定义，但推出它的具体实现也是很困难的。

最常用的计算平方根的方法为牛顿迭代法，其过程用如下代码表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(define (sqrt-iter guess x)
	(if (good-enough? guess x)
		guess
		(sqrt-iter (improve guess x) x)))

(define (improve guess x)
	(average guess (/ x guess)))

(define (average x y)
	(/ (+ x y) 2))

(define (good-enough? guess x)
	(< (abs (- (* guess guess) x)) 0.001))

(define (sqrt x)
	(sqrt-iter 1.0 x))

文字描述为不断使用一种方法猜测一个数，计算它的平方，使得平方值不断逼近给定的被开方数。

1.1.8 Procedures as Black-Box Abstractions

这一章讲述了将程序作为黑箱抽象的重要性。这个没啥好说的，好是很好，但不恰当地执行就容易变得更加抽象🤣。

  • 接口和实现分离：程序的接口（输入输出）和实现（内部细节）是分离的。用户通过接口使用程序，而不需要了解实现细节。
  • 信息隐藏：通过隐藏不必要的实现细节，可以减少认知负担，使程序更易于理解和使用。
  • 模块化设计：通过将程序分解为独立的模块，每个模块实现特定的功能，可以提高程序的可维护性和可扩展性。

1.2 Procedures and the Processes They Generate

在第一节讲述了什么是程序，但并没有讲该怎么写程序。这就相当于我们了解了下棋的规则，但还是不知道下棋的策略。这一节就是通过一些算法介绍一些常见的程序结构。(说实在的 sicp 的精华都在后几章，前面的太基础有点想跳过了…)

1.2.1 Linear Recursion and Iteration

这一小节通过计算阶乘介绍什么是递归和迭代结构。

定义阶乘:

n!=n×(n−1)×(n−2)×⋯×2×1n! = n \times (n-1) \times (n-2) \times \dots \times 2 \times 1

递归结构

根据数学定义，能够很容易地写出计算程序为:

1
2
3
(define (factorial n)
  (if ( = n 1) 1 ( * n (factorial (- n 1))) )
  )

根据 1.1.5 The Substitution Model for Procedure Application 中所讲的，上述程序展开的计算过程为如下图:

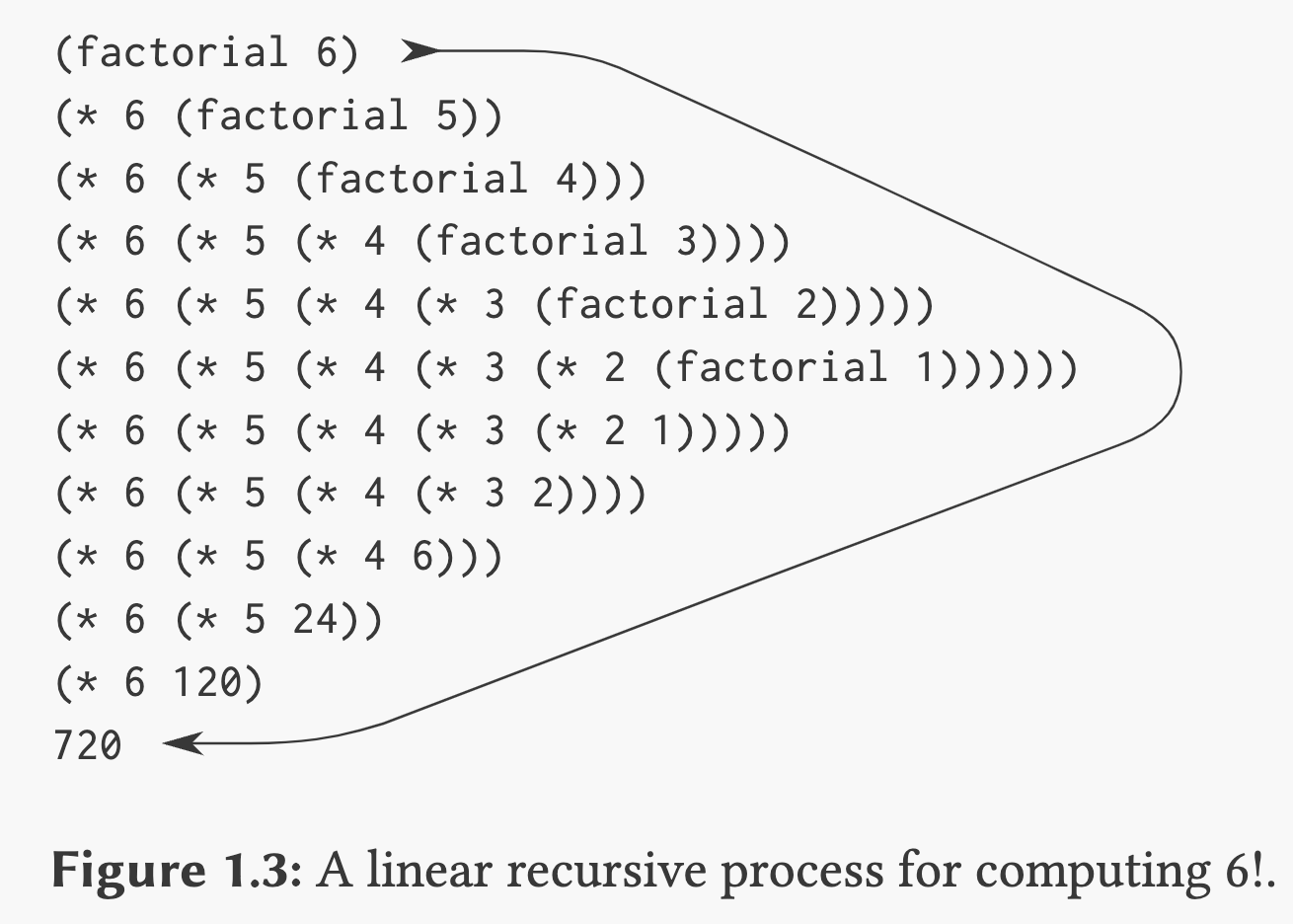
迭代结构

我们可以换个顺序计算阶乘, 从 11 开始乘，直到乘到 nn ，计算的程序为：

1
2
3
4
5
6
7
(define (factorial n)
  (factorial-iter 1 1 n)
  )

(define (factorial-iter res now max-iter-count)
  (if (= now max-iter-count) (* res now) ( factorial-iter (* res now) (+ now 1) max-iter-count ) )
  )

这个程序的展开计算过程为:

可以看出，计算同一个数学公式，上面两种的计算过程完全不同。

对于递归结构，它的表现是一种展开又收缩的过程，展开表现为程序构建了一系列的 “deferred operations”，收缩表现为在完全展开后这些运算的实际计算过程，解释器在计算的时候需要存储这些运算过程。在计算 n!n! 的时候，存储的表达式随着 nn 线性增长，这被称为线性递归结构。

与之相对应的，第二种计算过程为迭代计算结构，可看出，解释器并不需要保存运算的过程，需要保存的是变量 res now max-iter-count 。一般来说，迭代计算过程就是那种可以使用固定变量表达计算状态的过程，同时它还有一个从当前状态转移到下一个状态的过程，还有一个表达式表达这个计算过程何时终止。在计算 n!n! 的时候，计算的表达式随着 nn 线性增长，这种被称为线性迭代结构。

tips: 本章练习可以使用 trace 打印计算过程。

1.2.2 Tree Recursion

本小节通过计算斐波那契数列介绍树形递归结构，斐波那契数列为如下数列:

0,1,1,2,3,5,8,…0,1,1,2,3,5,8,\dots

满足如下定义:

F0=0F1=1Fn=Fn−1+Fn−2(n≥2) \begin{aligned} F_0 &= 0 \\ F_1 &= 1 \\ F_n &= F_{n-1} + F_{n-2} (n \ge 2 ) \end{aligned}

它的对应程序为

1
2
3
4
5
(define (fib n)
  (cond
    [(= n 0) 0]
    [(= n 1) 1]
    [else (+ (fib (- n 1)) (fib (- n 2)))]))

它的对应计算过程为:

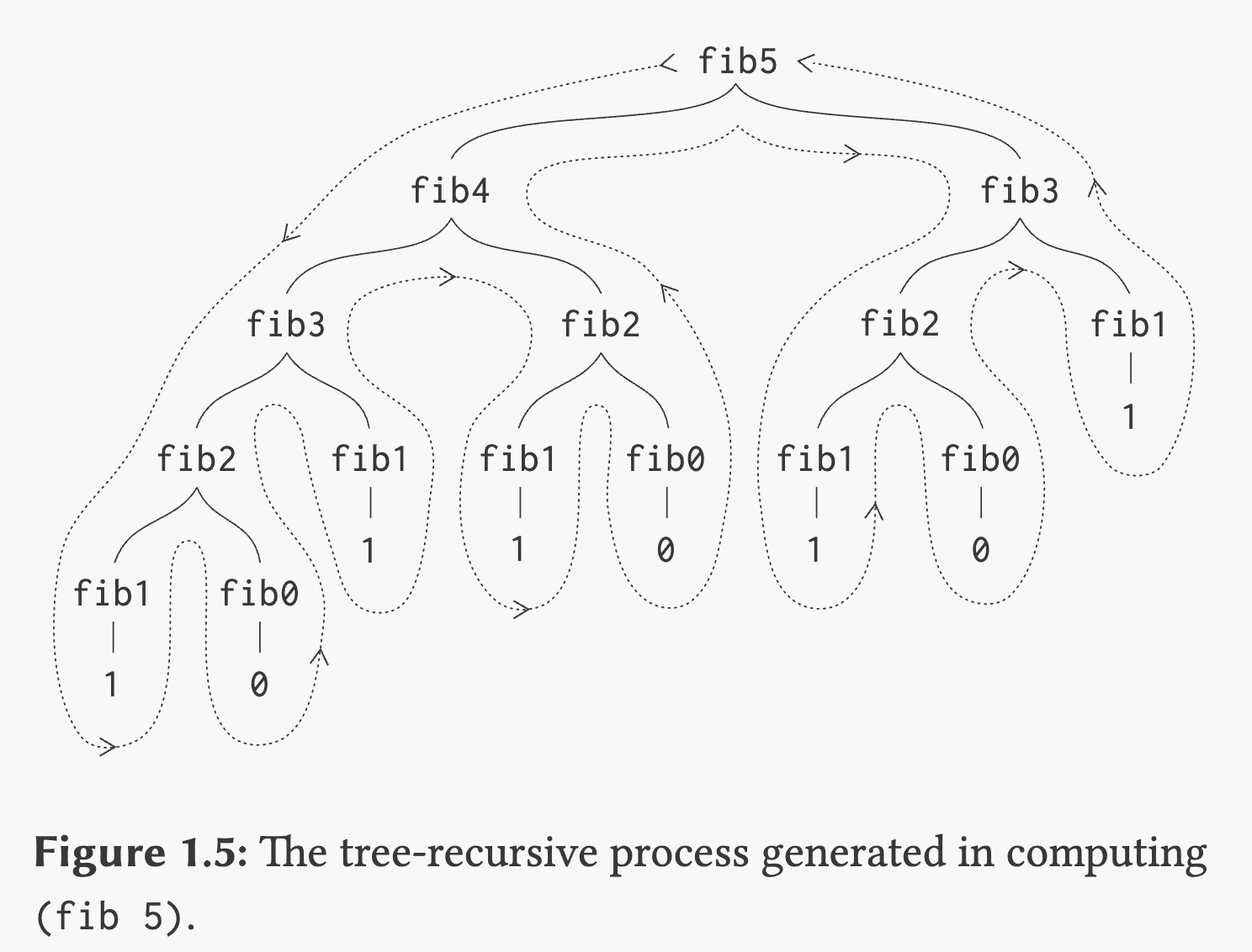
从计算图中可以看出，树形递归结构有许多冗余的计算，像 fib 2 就计算了三次。为了减少这种计算，我们可以使用一些变量存储当前计算的状态，下面的计算斐波那契数列的迭代结构:

1
2
3
4
5
(define (fib n)
  (fib-iter 0 1 n))

(define (fib-iter now next count)
  (if (= count 0) now (fib-iter next (+ now next) (- count 1))))

显然，这种方式计算 fib n 的时间复杂度是 O(n) 的。尽管后一种结构相较于第一种结构速度更优，但第一种是最直观的，迭代法 (动态规划) 的关键在于找到能够代表当前状态的一组变量，这往往是比较难想到的，书中之后就给了个分钱币的例子，使用树形递归能够很容易写出问题的递归形式，但迭代形式却相对困难，书中作为思考题。背包问题太基础了就不说了，跳过。

1.2.3 Orders of Growth

这章讲的是什么是时间复杂度，跳过吧

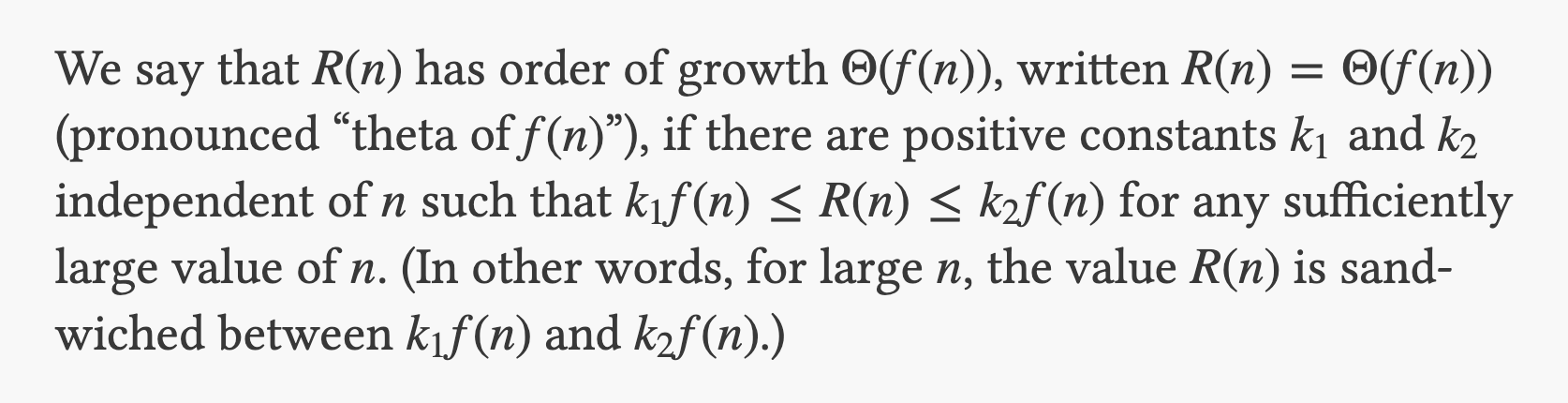
后面几节基本是在介绍一些基础的算法。

1.2.4 Exponentiation

介绍快速幂，跳了

1,2.5 Greatest Common Divisors

介绍计算最大公约数的方法，经典的 Euclid’s Algorithm，其中简略地提到了时间复杂度的证明方法：

1.2.6 Example: Testing for Primality

介绍素数检测的方法，根号下遍历 和 费马测试(这玩意写不写呢…)，

1.3 Formulating Abstractions with Higher-Order Procedures

在经过了一系列算法的洗礼后，我们需要换换口味，来了解一些更加偏向 pl 的知识。本节介绍的是对过程使用高阶函数进行抽象。(高阶函数本质就是能够接受函数作为参数的函数)

1.3.1 Procedures as Arguments

本节首先提出了一个场景: 计算 从 a 到 b 的和、平方和、指定序列和。常规来说可以写出如下代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(define (sum-integers a b)
  (if (> a b) 
      0 
      (+ a (sum-integers (+ a 1) b))))

(define (sum-cubes a b)
  (if (> a b) 
      0 
      (+ (cube a) 
         (sum-cubes (+ a 1) b))))

(define (pi-sum a b)
  (if (> a b)
      0
      (+ (/ 1.0 (* a (+ a 2))) 
         (pi-sum (+ a 4) b))))

显然，这些代码除了函数名和内部计算函数不同之外，其余的几乎没有区别，我们可以从数学的角度上看待这些过程: 数学上，对于 a 到 b 的求和可以表示为

∑n=abf(n)=f(a)+⋯+f(b)\sum_{n=a}^{b} f(n) = f(a) + \dots + f(b)

其中 f(n) 就是可以替换的函数。

对与如上的过程，我们可以写出如下的函数:

1
2
3
4
5
(define (sum term a next b)
  (if (> a b)
      0
      (+ (term a)
         (sum term (next a) next b))))

于是如上的过程可以被写成:

1
2
3
4
5
6
7
8
9
10
(define (inc n) (+ n 1))

(define (identity x) x)

(define (sum-integers a b)
  (sum identity a inc b))

(define (sum-cubes a b)
  (sum cube a inc b))

1.3.2 Constructing Procedures Using Lambda

介绍 lisp 匿名函数还有使用 let 创建局部变量，用于简化高阶函数的输入。

1.3.3 Procedures as General Methods

1.3.4 Procedures as Returned Values

🦻🦻🦻🦻🦻🦻🦻🦻